Reflection over the line y=x 253503-Reflection over the line y x calculator
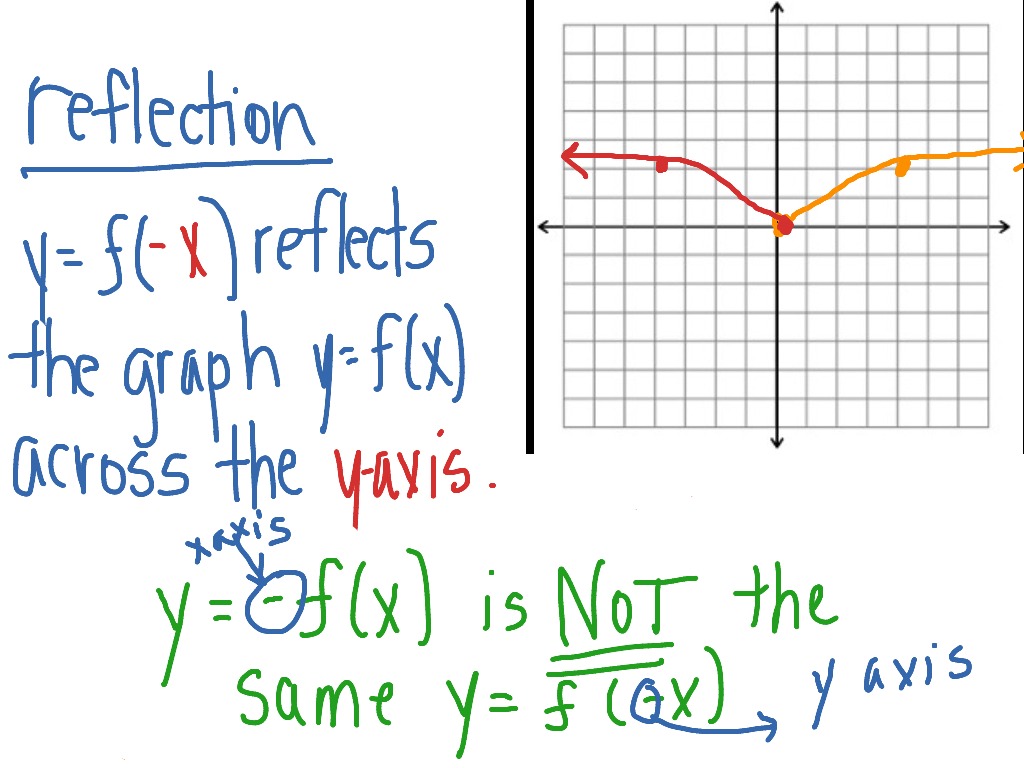
And b = 4 The corresponding linear transformation rule is (p, q) → (r, s) = (05p 0866q 3464, 0866p 05q – 2) Line y = 4/5x 4 θ = Tan1 (4/5) = 3866°A reflection (or flip) is one kind of transformation The reflection of a point is another point on the other side of a line of symmetry Both the point and its reflection are the same distance from the line The following diagram show the coordinate rules for reflection over the xaxis, yaxis, the line y = x and the line y = x Scroll downReflect over the y = x When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed)
Illustrative Mathematics
Reflection over the line y x calculator
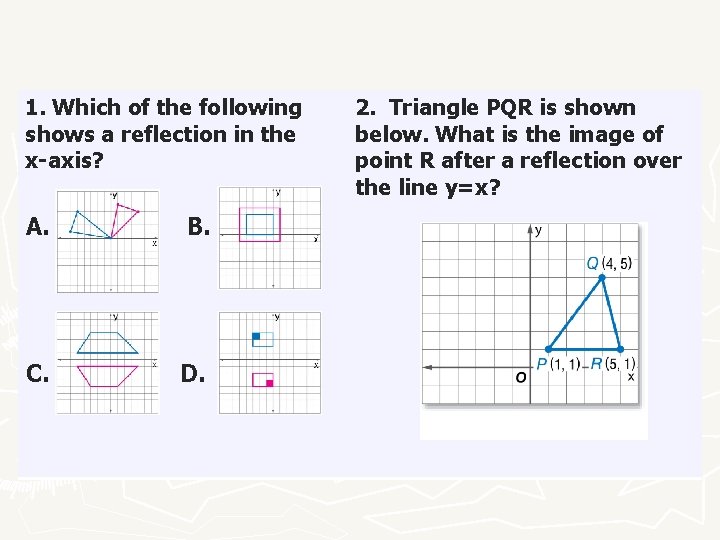
Reflection over the line y x calculator-ΔDEF with D (4,1), E (0,10) and F (1, 1) is reflected across the line y = x Which of the following are the correct coordinates for ΔD'E'F' answer choices D' (1, 4) E' (10, 0) F' (1, 1) D' (1, 4) E' (10,Reflection in the line y = x Try to work out the coordinates of the reflected points before you reveal the answer 1) If the point (2, 3) is reflected over the xaxis what is the new point?
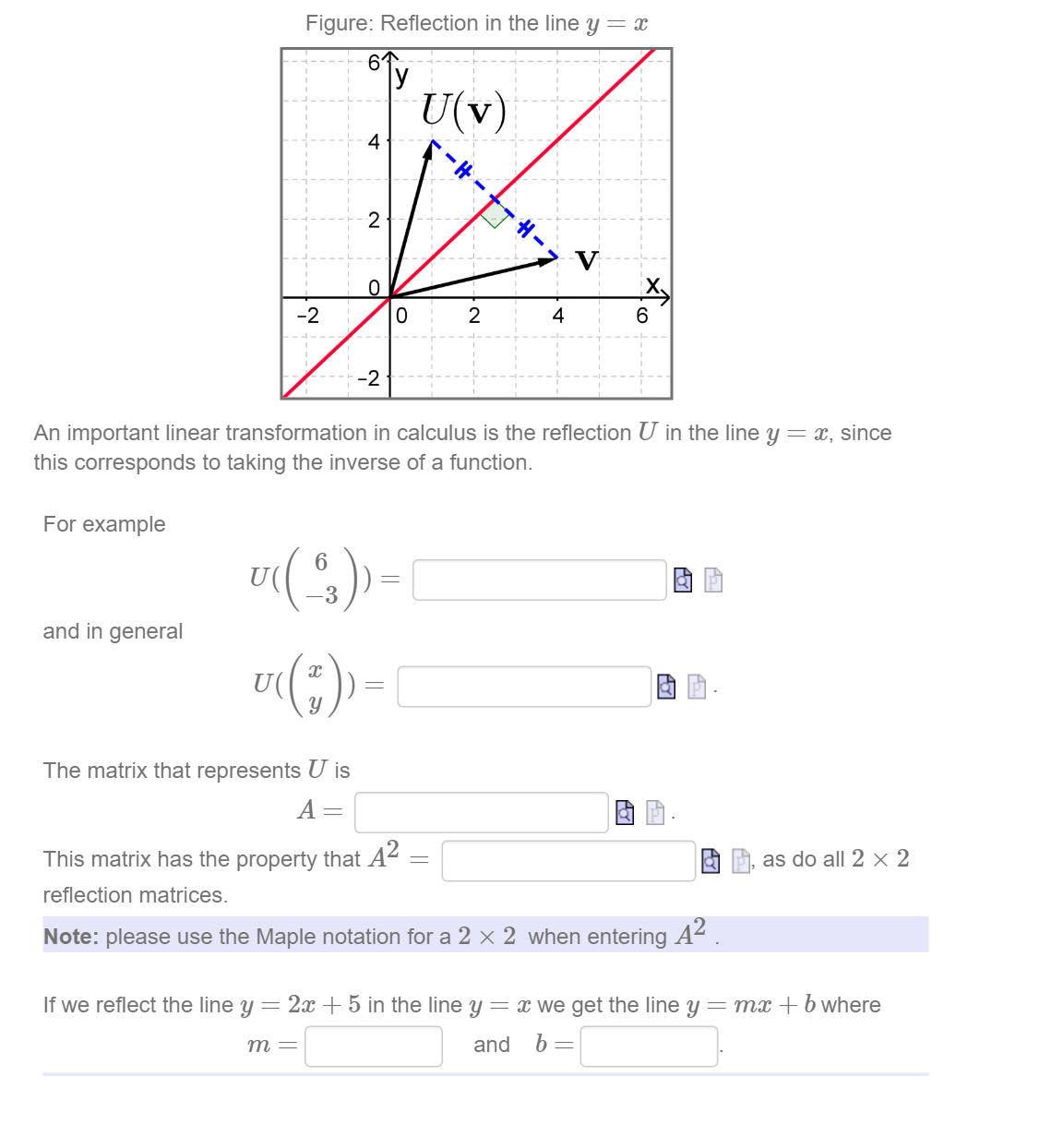



Solved An Important Linear Transformation In Calculus Is The Chegg Com
Explore the reflection of the red hexagon preimage over the yaxis, the xaxis and the line y = x Check the line to reflect the image about You can also modify the red hexagon by moving the vertices What do you think the rules should be for each reflection?This lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitterIn order to get to the expected transformation, first, flip it over the yaxis which cost 90 degrees of rotation Then lastly, flip shape from 2nd quadrant over the yaxis It will now be coincide with the transformation at the 3rd quadrant
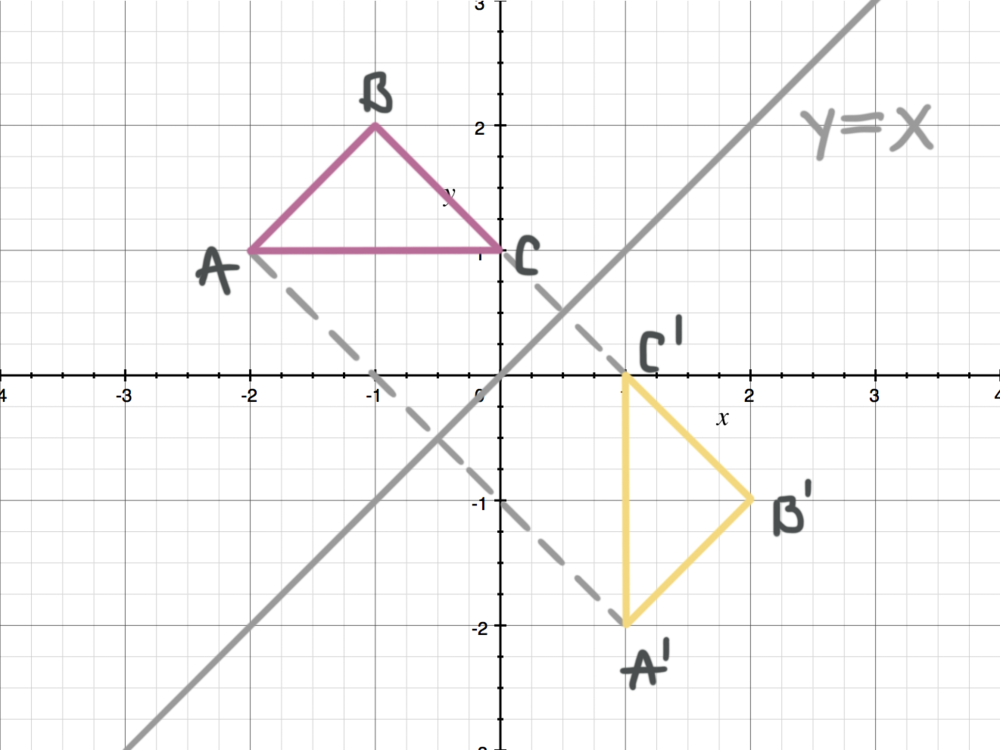
This brief video explores reflecting an image over the y=x and the y=x lines, with the coordinate rules for bothReflections (over xaxis, yaxis, y=x, and line x=2)A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3) All of the points on triangle ABC undergo the same change to form DEF
Image A' = (5 , 3 ) Any point (x , y ) when reflected in the line y = x has an image ( y , x ) example A (3 , 4 ) has image A' ( 4 , 3 ) Precalculus Science Anatomy &( x, y) >Geometry 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1



Geometric Reflections Q35 50 Intro To Geometry



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download
Reflections across y=x Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinatesAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &Reflections over the line y= x Discover Resources roller coaster graph;




Reflection Over The Line Y X Geogebra




Reflections Through The Axes And The Lines Y X And Y X Geogebra
Basic Trig Graphing OpenIf you need the visible reflection then you can use package pstoptic Run the example with pdflatex shellescape <file>Discover Resources Carnot cycle ( with energies and efficiency) Locating the Real Roots of a
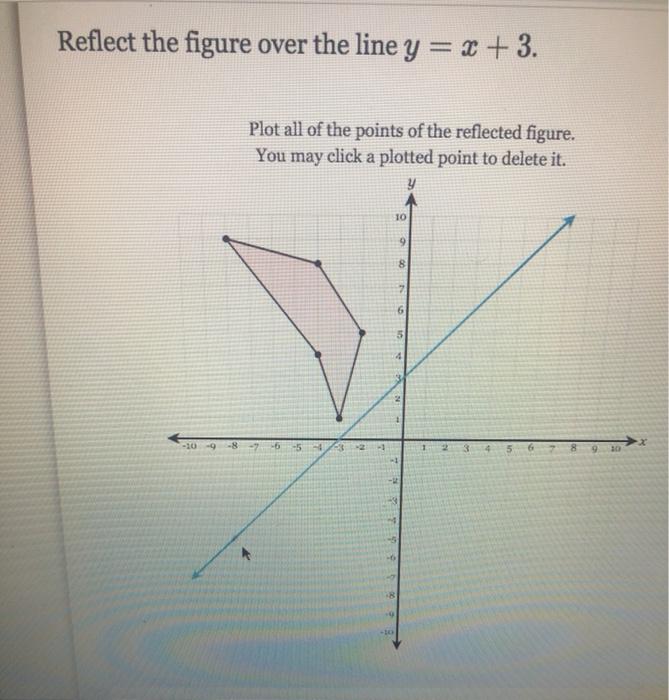



Solved Reflect The Figure Over The Line Y X 3 Plot All Chegg Com



Illustrative Mathematics
Play this game to review Mathematics What is the rule for a reflection across the y = x line?Reflection over Y=X Author Jason Wofsey Topic Reflection Drag the points from triangle ABC to create it's image after a reflection over the line Y = X New Resources Quiz Graphing Exponential Functions (Transformations Included) Parent Sine and Cosine Functions;This video demonstrates how to reflect a figure over the line y=x It shows two methods of reflecting over y=x The video shows how to count towards the y=x




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
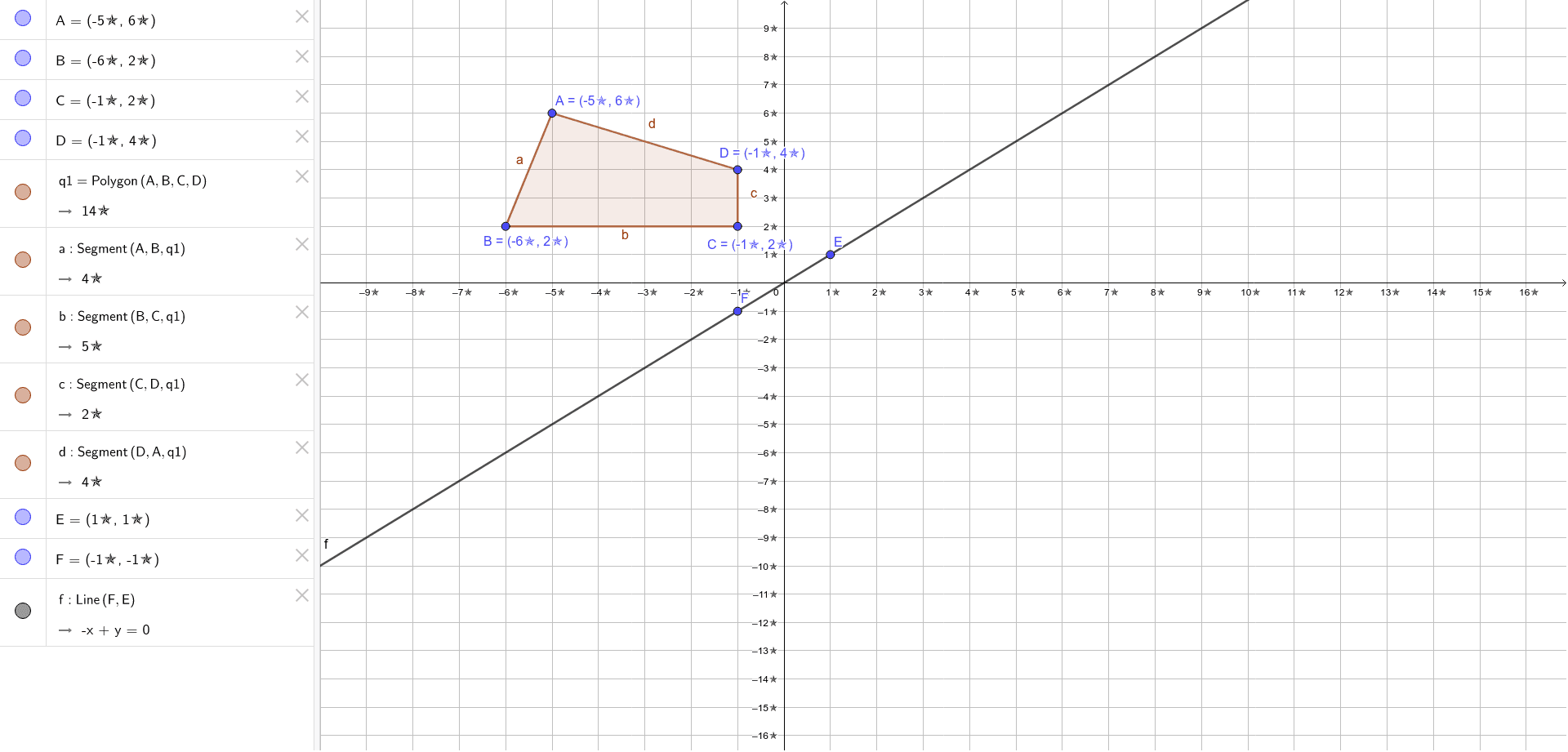



Reflection Across The Line Y X Geogebra
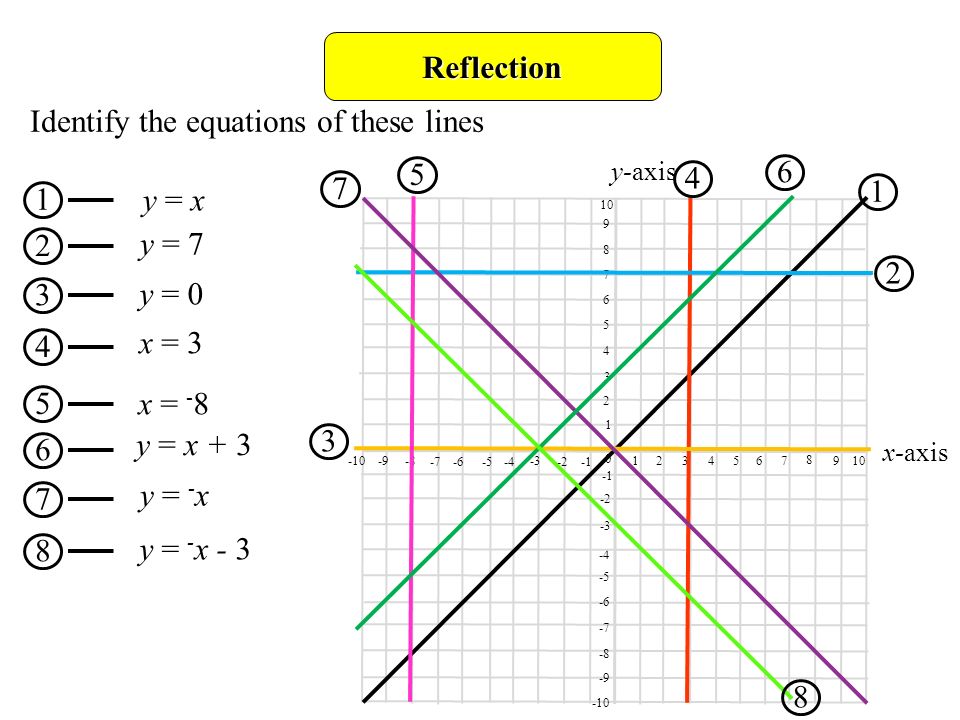
Reflecting over Any Line When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure In other words, the line x = 2 (line of reflection) lies directly in the middle between the original figure and its image And also, the line x = 2 (line of reflectionReflecting over the line y = x When the reflect a point across the line y = x , the x coordinate and the y coordinate change places Reflection is (3,4)Reflection over the yaxis Author user Topic Reflection Reflection over the yaxis New Resources Pythagorean Tiling;



Warmup Reflect Triangle Abc Across The Line Y




Reflections
Begin with the reflection though the yaxis Try to guess which ordered pair rule will produce the desired image Next try a reflection through the xaxis For this step you will need to drag the red X to the xaxis (a blue open circle point is plotted as a suggestion) Now the hard part Can you match which rules reflect over the lines y=x and y=x?Learn how to reflect over the y=x line ex 3 Learn how to reflect over the y=x line ex 3 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortlyPositions of cards while shuffling (in a standard deck of 52 cards) Dice Rolling Simulation (2) Discover Resources Barycentre1;



Solved Translations Multiple Choice Question A Reflection Over The Line Y X B Reflection Over The X Axis C Reflection Over The Y Axis D Transla Course Hero




Reflections Geometry Abroad
And b = 4 TheLet's talk about reflections over this line When we reflect a point in the xy plane over the line y equals x, the image has the x and ycoordinates switched So, here, 2, 5 and 5, 2 are reflected images of each other over the line y equals x In other words, we swap the place of the xcoordinate and the ycoordinateExploring effects of k



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N



Learn About Reflection Over A Horizontal Or Vertical Line
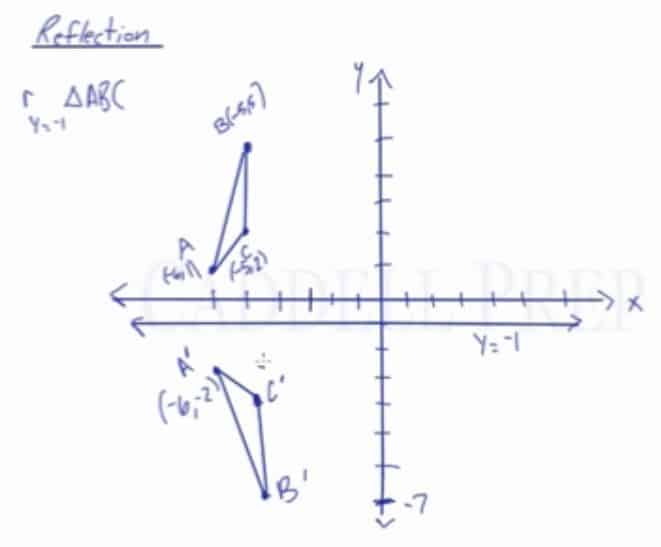
Answer (1 of 3) This is a method used to find the reflection over the line y = x, aka finding the multiplicative inverse of elementary functions for a function y of x, switch your x and y variables solve for y That gives us the reflection For example, if we had y = 3x 6, switch x and yReflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change sizeApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflection We'll be



Solution What Is The Image Of A 3 1 After A Reflection First Across The Line Y 3 And Then Across The Line X 1




Transformation Reflection Over The Line Y X Youtube
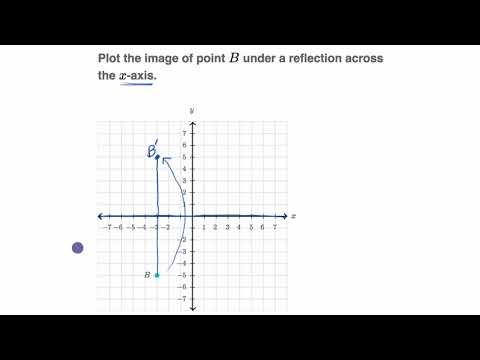
Safety How works Test new features Press Copyright Contact us Creators( x, y) ( x, y ) >A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y Axis A reflection of a point, a line, or a figure in the Y axis involved reflecting the image over the Y axis to create a mirror image



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com
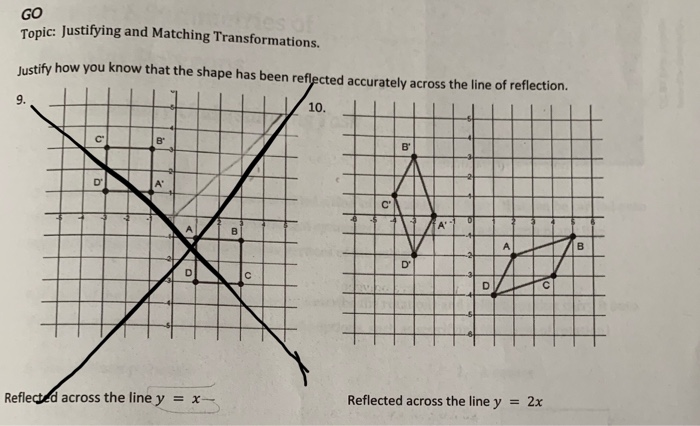



Solved Go Topic Justifying And Matching Transformations Chegg Com
GeoGebra News September 21 ;Answer (1 of 10) Here is another elegant way of looking at this, in addition to the answers below which are all correct Given a point (x, y) , we want a point (y, x) So, the question is \forall (x, f(x)) , what is the line of symmetry, \ni , (f(x), x) is constructed Notice the distance beThis allows you to reflect the function on an arbitrary line and without being restricted in your choice of compilers a=b=1 is the x=y line




Reflection Mathbitsnotebook A1 Ccss Math




Geometry Reflection Across Y X Youtube
2) If the point (4, 6) is reflected over the yaxis what is the new point?When reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x =(y,x) For example For triangle ABC with coordinate points A(3,3), B(2,1), and C(6,2), apply a reflection overPhysiology Astronomy Astrophysics Biology Chemistry Earth Science Environmental Science Organic Chemistry Physics Math Algebra Calculus Geometry Prealgebra Precalculus Statistics Trigonometry




Reflection Over The Y X Line Youtube




Solved An Important Linear Transformation In Calculus Is The Chegg Com
A shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinateClick here 👆 to get an answer to your question ️ Please help me !!!Perpendiculars from a Point;




Picture Of Reflection Across Y Axis Reflection Math Math Reflection




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
Two open blue circles are plotted to help youA reflection of a point over the line y = − x is shown The rule for a reflection in the origin is ( x , y ) → ( − y , − x ) Subjects Near Me Series 52 Test Prep Research Writing Tutors IB Visual Arts SLRads and Revs Quick Conceptual Insight;




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



How Are We Studying Transformations Differently
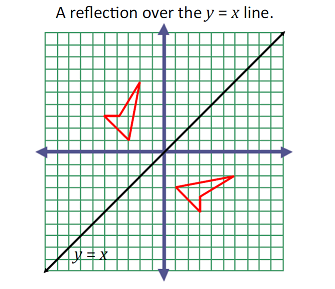
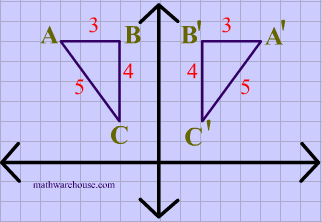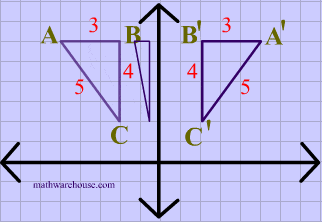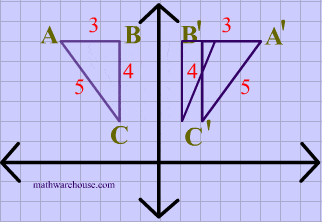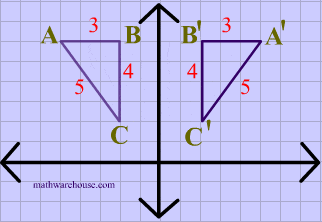
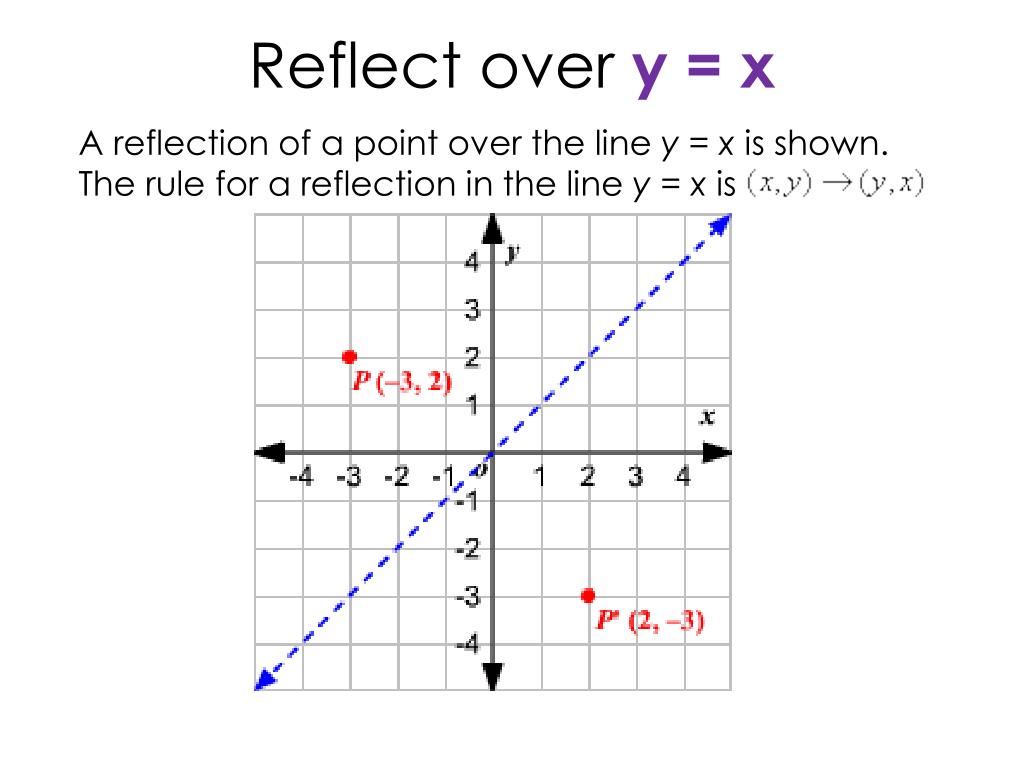
GeoGebra News September 21;Remember this is a negative diagonal line through the origin Remember this is a </strong><strong style=color rgb(241, 77, 118);>negative </strong><strong>diagonal line through the origin</strong></p>Reflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you want
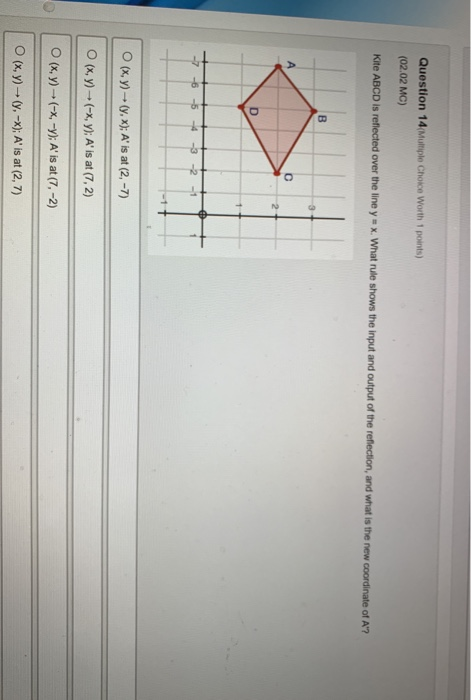



Solved Question 14 Multiple Choice Worth 1 Points 02 02 Chegg Com



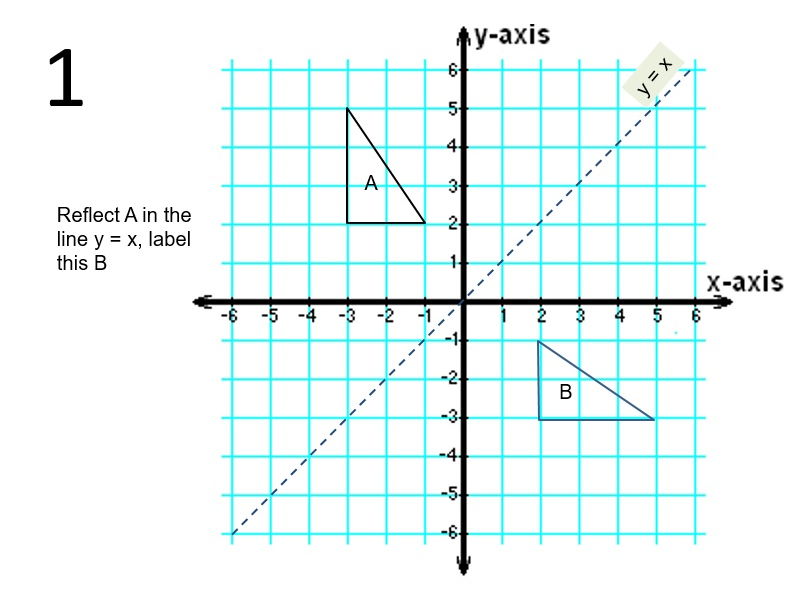
1
Diagonals of a Rectangle;What is the image of (8,1) after a reflection over the line y = x?The correct answer for this question is reflect over the yaxis, reflect over the xaxis, rotate 180°



Diagonal Reflections In The Line Y X Teaching Resources



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
Reflection over the line y=x Author Kerry Gallagher, user, Josh Topic Reflection Reflection over the line y=x New Resources Parabola, Focus, Directrix;Transformation Reflection (across y = x) This video is a demonstration of how a reflection can take place across a line where y=xThe handout, Reflection over Any Oblique Line, shows the derivations of the linear transformation rules for lines of reflection y = √(3)x – 4 and y = 4/5x 4 Line y = √(3)x – 4 θ = Tan1 (√(3)) = 60°




Kite Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection Brainly Com




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
Thus the reflection of the point ( 3, 2) over the line {eq}y = x {/eq} is the point (2, 3) In this point x coordinate is positive and y coordinate is negative that means this point belongs




Reflect The Figure Over The Line Y 1 Which Is Point A After The Reflection 2 X A 3 1 O A 3 Brainly Com




Reflection Over Y 2 With Rule Educreations
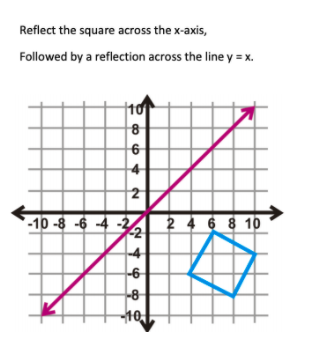



Solved Reflect The Square Across The X Axis Followed By A Chegg Com




Reflection Over The Line Y X Math Showme
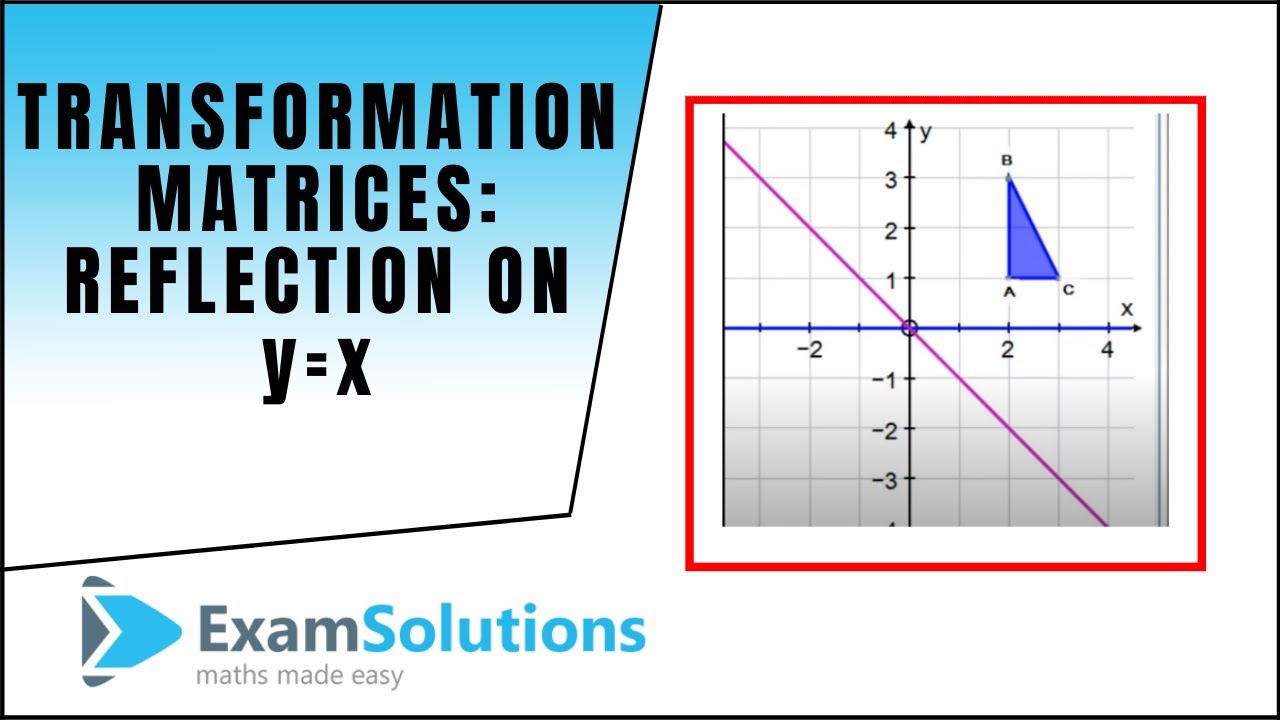



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube




Reflection Over The Line Y X Youtube
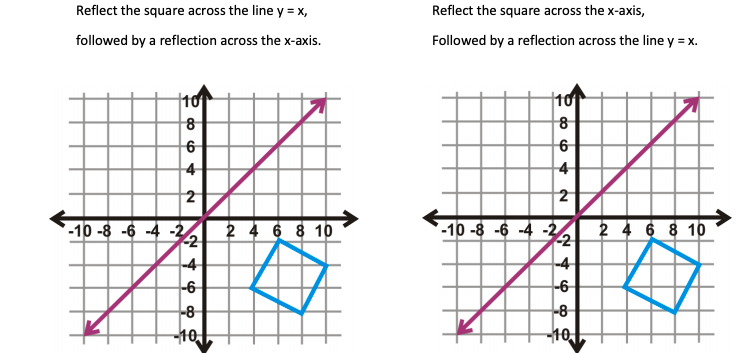



Solved Reflect The Square Across The Line Y X Followed By Chegg Com



1




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflection Mathbitsnotebook A1 Ccss Math



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id



Reflections Review Article Reflections Khan Academy




Reflection Mathbitsnotebook A1 Ccss Math




Write The Coordinates Of The Vertices After A Reflection Across The Line Y X Brainly Com




How To Find A Reflection Image




Write The Coordinates Of The Vertices After A Reflection Over The Line Y 3 Brainly Com




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflection Over A Line Expii




Ixl Reflections Find The Coordinates Grade 7 Maths Practice




Reflection In The Line Y X Transformation Matrix Youtube




Reflection In The Line Y X Geogebra




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Math Alive Geometry 1



Reflection Of A Point In A Line Msrblog




Linear Transformations With Matrices Lesson 10 Reflection In The Line Y X Youtube
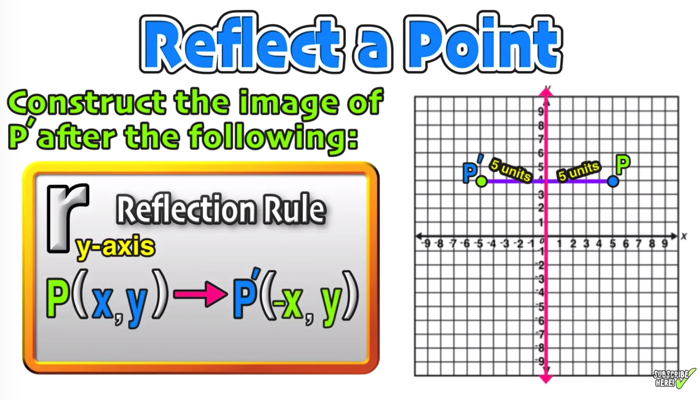



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Over Y X Math Geometry Showme
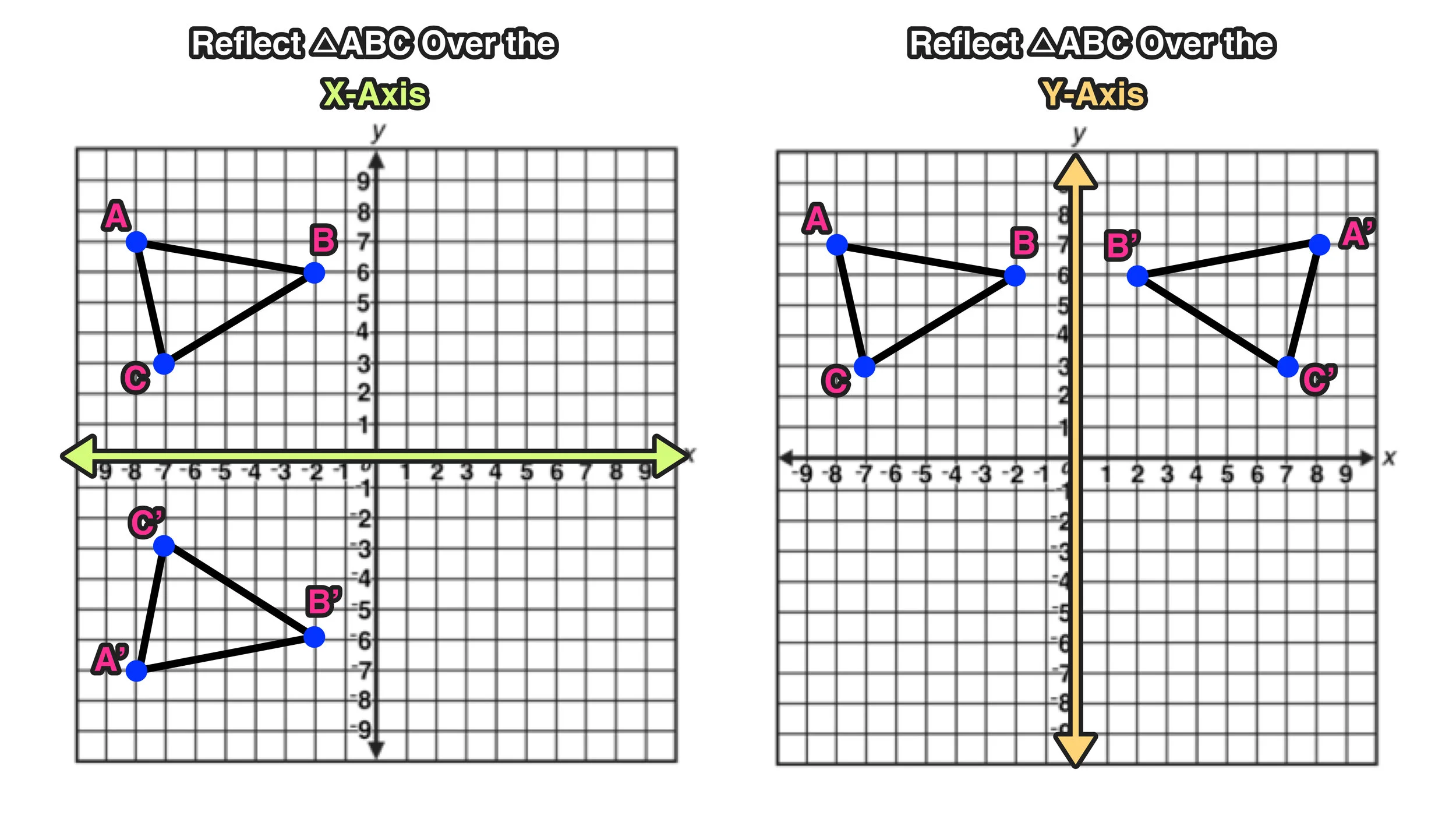



Reflection Over The X And Y Axis The Complete Guide Mashup Math
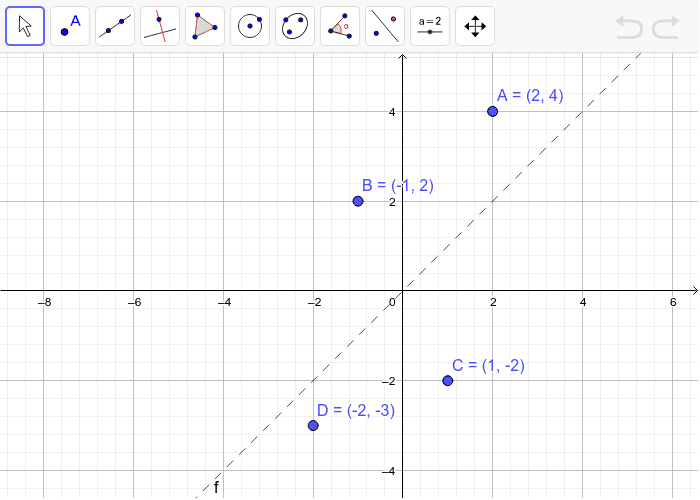



Reflecting In The Line Y X 2 Geogebra
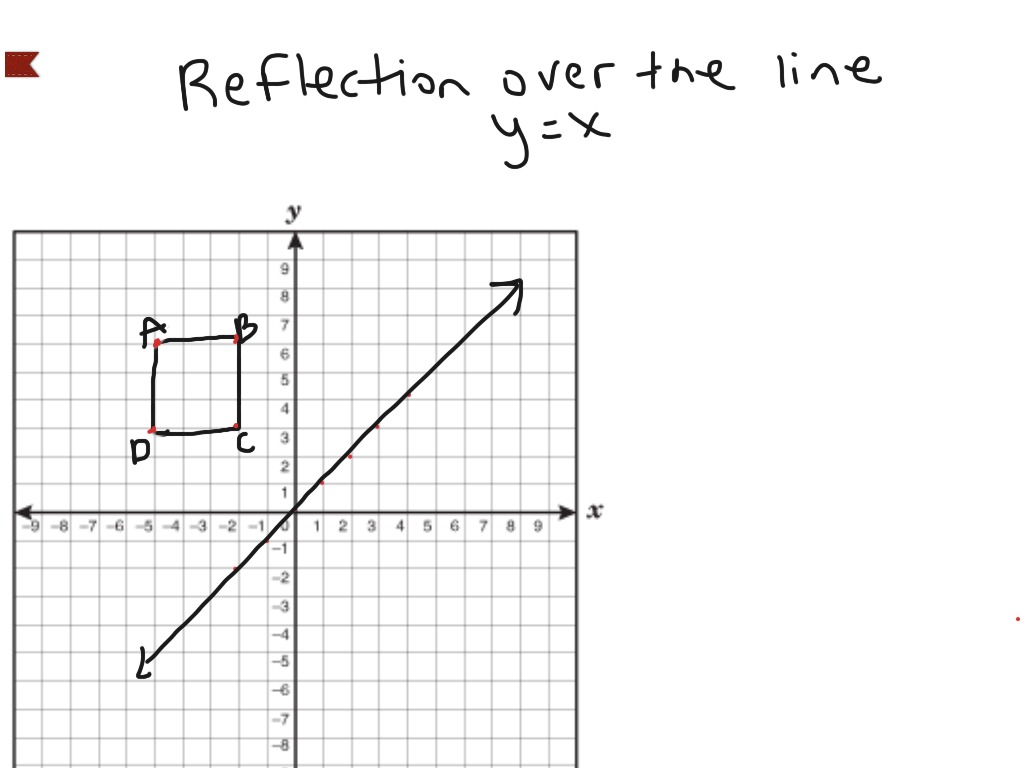



Reflection Over The Line Y X Math Showme



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com



Solution Abc Is Reflected About The Line Y X To Give A 39 B 39 C With Vertices A 39 1 1 B 39 2 1 C 1 0 What Are The Vertices Of Abc 39




02 02 Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Brainly Com



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Which Graph Shows A Reflection Across The Line Y X Brainly Com
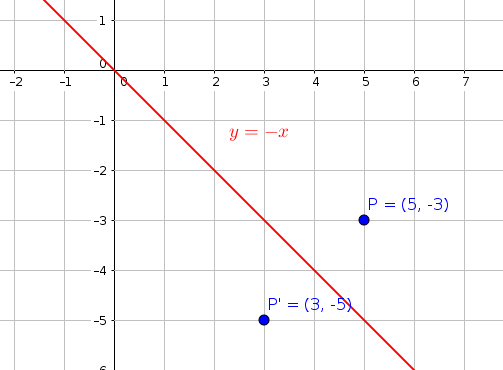



What Is The Reflection Image Of 5 3 In The Line Y X Socratic
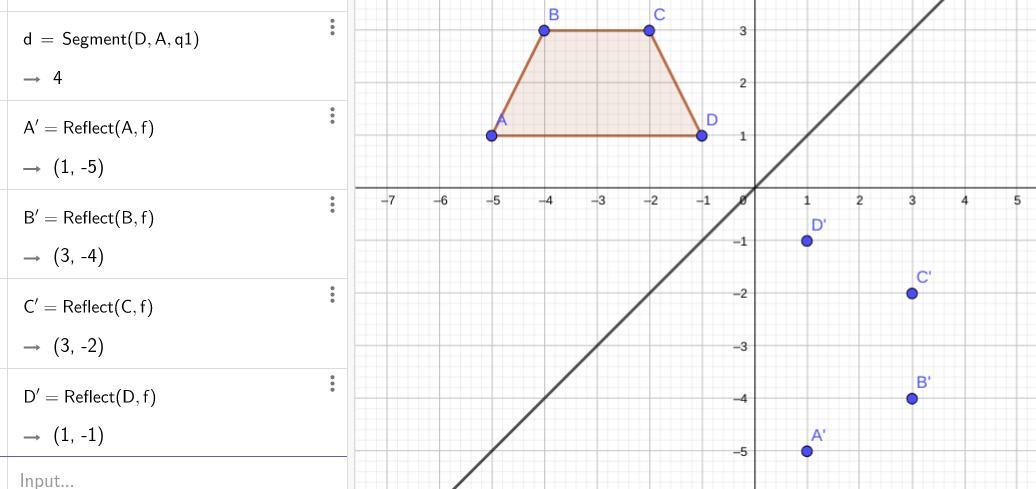



Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection And What Is The New Coo
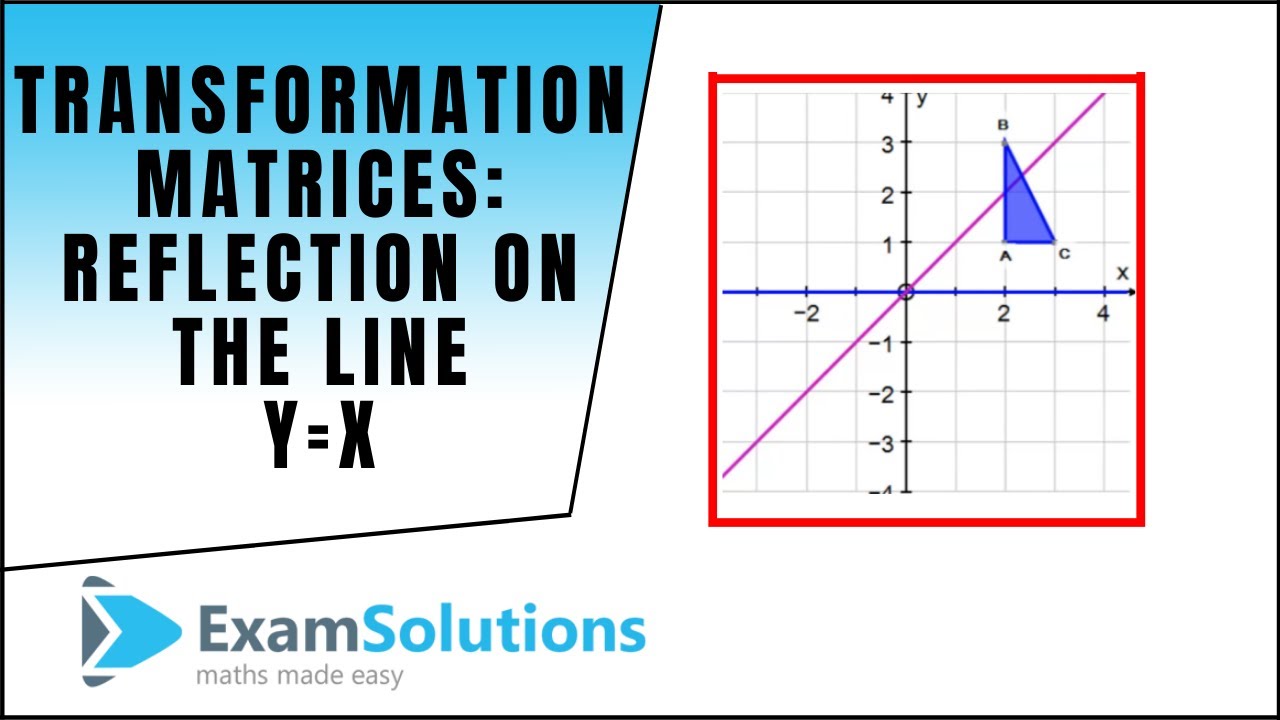



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



Reflection Across The Y Axis Math Functions Showme



Reflecting Points Video Reflections Khan Academy



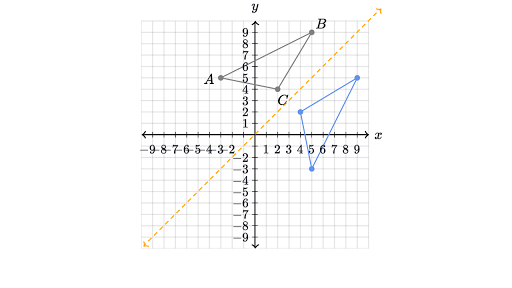
Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Common Reflections Key Stage 3




Learn About Reflection Over The Line Y X Caddell Prep Online



Math Alive Geometry 1




What Is A Line Of Reflection Printable Summary Virtual Nerd




Reflection Transformation Matrix




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor



3



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download
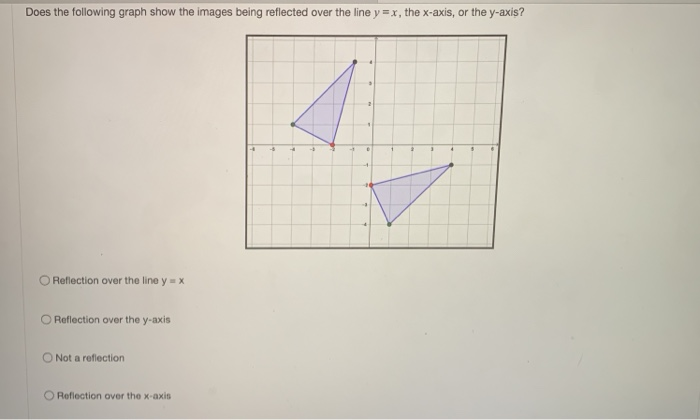



Solved Does The Following Graph Show The Images Being Chegg Com



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q
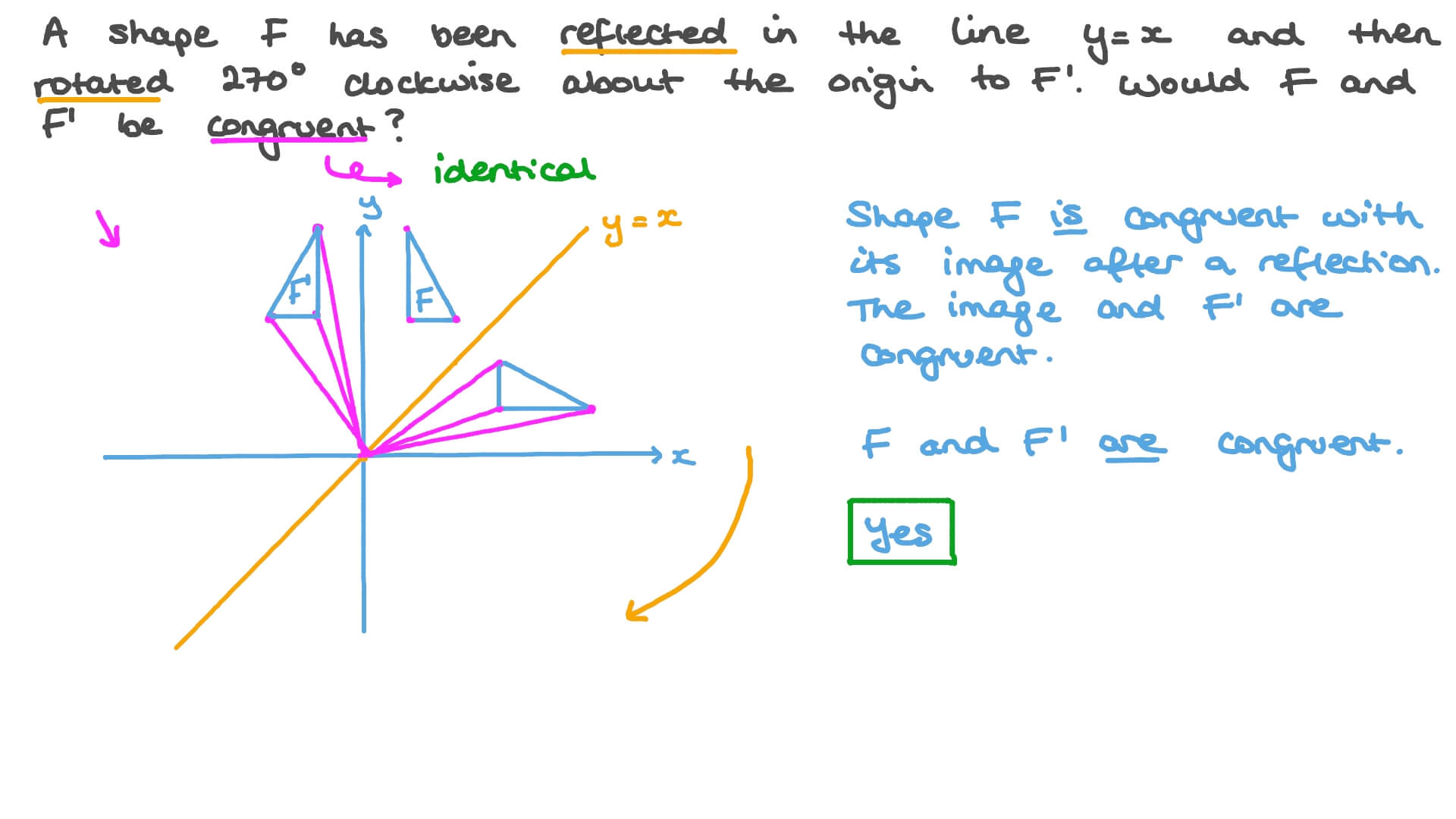



Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics



What Is The Image Of 2 5 Reflected Across X 2 Socratic
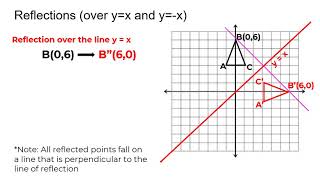



Reflection Over The Y X Line Youtube




Reflection Transformation Matrix
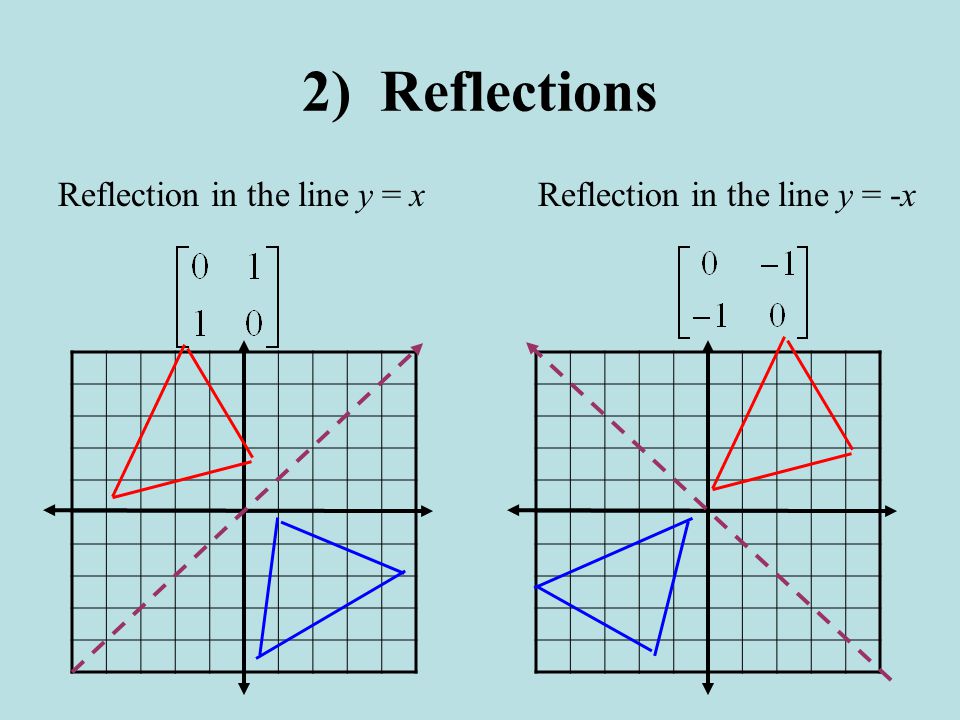



4 4 Transformations With Matrices Ppt Video Online Download
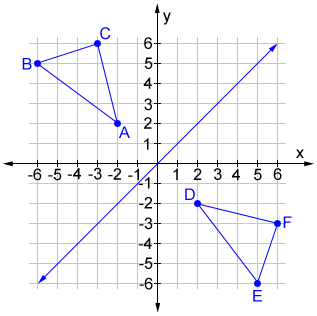



Reflection




Reflection Transformation Matrix




Transformations Of Graphs



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflections Ck 12 Foundation



Reflection Across X 1




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




How To Find A Reflection Image
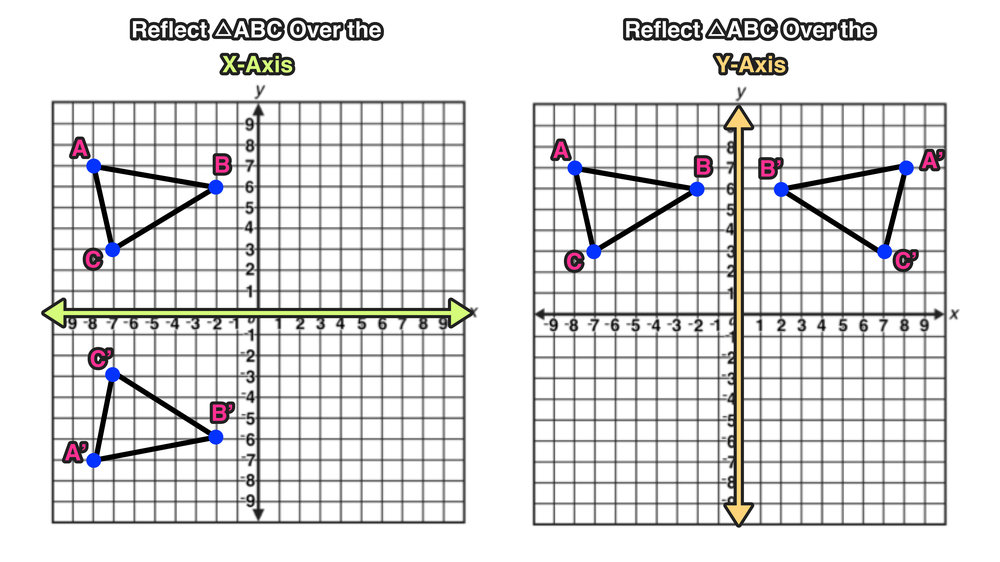



Reflection Over The X And Y Axis The Complete Guide Mashup Math
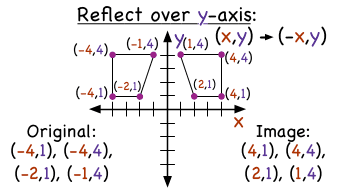



How Do You Use Coordinates To Reflect A Figure Over The Y Axis Virtual Nerd



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora




Reflections Across Y X Geogebra



What Does It Mean To Reflect Over The Y X Line Quora
コメント
コメントを投稿